【素数筛法小结】fzu 1607 + fzu 1753
日期:2011-11-17
点击:173
来源: 基德KID.1412
http://acm.fzu.edu.cn/problem.php?pid=1607
题意:求n平均分成m份(m>1),问有多少种分法,以及平均的分量最多可以达到多少?
多少种分法:
求n的因子的组合数即可,由于m>1所以【所有因子取0个的情况不包括】
例如:n中有3个素因子p1,2个素因子p2,p1可以取0个,1个,2个,3个【4种情况】,p2可以取0个,1个,2个【3种情况】,所以分法 = 4*3-1 = 11
平均达到最大值:
n/(n的最小素因子)
http://acm.fzu.edu.cn/problem.php?pid=1753
题意:求多个组合数的最大公约数
思路:求各组组合数的各个素因子个数,以少为主,因为要的是公约数嘛,最后乘起来即可

求N!里包含某素数因子p的个数,就可以这样求。
while(n>0)
{
x+=n/p;
n/=p;
}
不理解请看:求N!的素因子个数的一个例子:
http://972169909-qq-com.iteye.com/blog/1126188
题意:求n平均分成m份(m>1),问有多少种分法,以及平均的分量最多可以达到多少?
多少种分法:
求n的因子的组合数即可,由于m>1所以【所有因子取0个的情况不包括】
例如:n中有3个素因子p1,2个素因子p2,p1可以取0个,1个,2个,3个【4种情况】,p2可以取0个,1个,2个【3种情况】,所以分法 = 4*3-1 = 11
平均达到最大值:
n/(n的最小素因子)
#include <iostream> using namespace std; #define M 1000005 int pf[M]; //pf[i]储存i的最大素因子 bool hash[M]; int main() { int i, j, n, k = 0, a, b, tp, q; bool flag; /******************素数筛法******************/ for (i = 2; i < M; i++) { if (!hash[i]) { pf[i] = i; for (j = i << 1; j < M; j += i) if (!hash[j]) hash[j] = true, pf[j] = i; } } /******************素数筛法******************/ while (~scanf ("%d", &n)) { flag = false; a = b = 1; while (n > 1) //将n进行素数分解 { tp = 1; q = pf[n]; //获取n的最大因子 while (n % q == 0) //求有多少个q因子 { n /= q; if (n > b) //b是拿到的最多的分量 b = n; tp++; } a *= tp; //简单组合数学 } printf ("%d %d\n", a-1, b); } return 0; }
http://acm.fzu.edu.cn/problem.php?pid=1753
题意:求多个组合数的最大公约数
思路:求各组组合数的各个素因子个数,以少为主,因为要的是公约数嘛,最后乘起来即可

求N!里包含某素数因子p的个数,就可以这样求。
while(n>0)
{
x+=n/p;
n/=p;
}
不理解请看:求N!的素因子个数的一个例子:
http://972169909-qq-com.iteye.com/blog/1126188
#include <iostream> using namespace std; #define LL __int64 #define inf 0x3fffffff #define M 100005 int p[10005], num[M], ni[155], mi[155]; //num[i]表示所求中有多少个i因子 bool flag; int main() { LL ans; memset (num, 0, sizeof(num)); int i, j, k = 0, t, n, m, tp, count, mins; /***********素数筛法***********/ /**********M以内的素数存到p数组**********/ for (i = 2; i < M; i++) { if (!num[i]) { p[k++] = i; for (j = i << 1; j < M; j+=i) if (!num[j]) num[j] = 1; } } /**********M以内的素数存到p数组**********/ /***********素数筛法***********/ while (~scanf ("%d", &t)) { memset (num, -1, sizeof(num)); mins = inf; for (i = 0; i < t; i++) { scanf ("%d%d", ni+i, mi+i); if (mins > ni[i]) //这个是必须的,自己想! mins = ni[i]; } for (j = 0; j < t; j++) { n = ni[j]; m = mi[j]; for (i = 0; i < k; i++) { if (p[i] > mins) //必须的! break; count = 0; /*****n!中有多少个p[i]*****/ if (n >= p[i]) { tp = n; while (tp) { tp /= p[i]; count += tp; } } /*****m!中有多少个p[i]*****/ if (m >= p[i]) { tp = m; while (tp) { tp /= p[i]; count -= tp; //因为是分母,所以减 } } /*****(n-m)!中有多少个p[i]*****/ if (n - m >= p[i]) { tp = n - m; while (tp) { tp /= p[i]; count -= tp; } } /****得到的count就是该组合数中有多少个p[i]****/ if (num[p[i]] == -1 || count < num[p[i]]) num[p[i]] = count; } } ans = 1; for (i = 0; i < k; i++) { if (num[p[i]] <= 0) continue; for (j = 0; j < num[p[i]]; j++) ans *= p[i]; } printf ("%I64d\n", ans); } return 0; }
- 查看图片附件
Tags:
相关文章列表:
推荐内容
最新文章
- hdu 2054 A==B?(模拟题)
- fzu 2065 数字判别(模拟题)
- Makefile的模板
- [推荐] 《Visual C++游戏开发经典案例详解》开发视频+
- jni初级(一)
- FOJ月赛-2011.12
- 互联网公司面试题之四
- hdu 4041 Eliminate Witches(模拟题)
- hdu 1237 简单计算器
- Codeforces Beta Round #97 (Div. 2) 【完整题解】
- 【BKDR_hash】HDU 2468 Shopping
- 【三分】HDU 2241 考研路茫茫——早起看书
- TBB(Intel Threading Building Blocks)学习笔记
- [C++] C++一步步从入门到成熟高手学习步骤与其所涉及
- hdu 4082 Hou Yi\'s secret(亚洲赛北京赛区B题)
关于我们 - 联系我们 - 广告服务 - 友情链接 - 网站地图 - 版权声明 - 发展历史

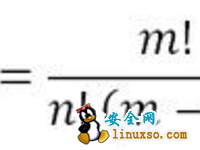

![[C++] C++一步步从入门到成熟高手学习步骤与其所涉及的所有书籍](/uploads/allimg/111209/1623163351-0-lp.jpg)